Codeforces 484 E. Sign on Fence

Bizon the Champion has recently finished painting his wood fence. The fence consists of a sequence of n panels of 1 meter width and of arbitrary height. The i-th panel’s height is hi meters. The adjacent planks follow without a gap between them.

After Bizon painted the fence he decided to put a “for sale” sign on it. The sign will be drawn on a rectangular piece of paper and placed on the fence so that the sides of the sign are parallel to the fence panels and are also aligned with the edges of some panels. Bizon the Champion introduced the following constraints for the sign position:

The width of the sign should be exactly w meters.
The sign must fit into the segment of the fence from the l-th to the r-th panels, inclusive (also, it can’t exceed the fence’s bound in vertical direction).

The sign will be really pretty, So Bizon the Champion wants the sign’s height to be as large as possible.

You are given the description of the fence and several queries for placing sign. For each query print the maximum possible height of the sign that can be placed on the corresponding segment of the fence with the given fixed width of the sign.

Input

The first line of the input contains integer n — the number of panels in the fence (1 ≤ n ≤ 105).

The second line contains n space-separated integers hi, — the heights of the panels (1 ≤ hi ≤ 109).

The third line contains an integer m — the number of the queries (1 ≤ m ≤ 105).

The next m lines contain the descriptions of the queries, each query is represented by three integers l, r and w (1 ≤ l ≤ r ≤ n, 1 ≤ w ≤ r - l + 1) — the segment of the fence and the width of the sign respectively.

Output

For each query print the answer on a separate line — the maximum height of the sign that can be put in the corresponding segment of the fence with all the conditions being satisfied.

Examples

input

output

Note

The fence described in the sample looks as follows:

The possible positions for the signs for all queries are given below.

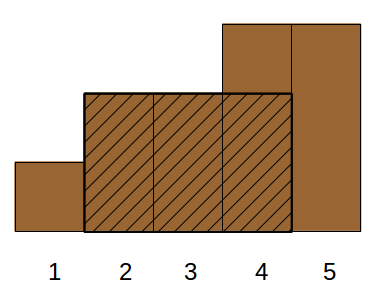The optimal position of the sign for the first query.The optimal position of the sign for the second query.

The optimal position of the sign for the third query.

Solution

题目大意：询问在[l,r]中所有长度为w的区间中小值最大为多少。

二分 + 可持久化线段树

假设我们二分到了一个答案mid，将所有大于等于mid的数标记为1,否则为0，如果[l,r]中最长连续1串比w小，mid非法，否则合法。

我们可以用可持久化线段树来预处理出0/1的数组，root[i]表示高度为i时的0/1线段树。每条线段维护最长1后缀、最长1前缀和最长连续1串。询问的时候合并一下log n条线段上的信息即可。

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
#include <cstdio>
#include <algorithm>
#include <map>
#define MP make_pair
using namespace std;
const int N = 100005;
const int mxlog = 22;
typedef pair<int, int> PII;
map<int, int> M;
struct List { int data, next; } list[N];
int fst[N], cnte, H[N], siz[N*mxlog], lc[N*mxlog], rc[N*mxlog], mx[N*mxlog], suf[N*mxlog], pre[N*mxlog], root[N], tot, cnt, ans, n, A[N];
int getint() {
    int r = 0, k = 1; char c = getchar();
    for (; c < '0' || c > '9'; c = getchar()) if (c == '-') k = -1;
    for (; '0' <= c && c <= '9'; c = getchar()) r = r * 10 - '0' + c;
    return r * k;
}
void ins(int idx, int dat) {
	list[++cnte].data = dat;
	list[cnte].next = fst[idx];
	fst[idx] = cnte;
}
void Update(int now) {
	pre[now] = pre[lc[now]] + (pre[lc[now]] == siz[lc[now]] ? pre[rc[now]] : 0);
	suf[now] = suf[rc[now]] + (siz[rc[now]] == suf[rc[now]] ? suf[lc[now]] : 0);
	mx[now] = max(max(mx[lc[now]], mx[rc[now]]), suf[lc[now]] + pre[rc[now]]);
}
void Change(int &x, int y, int l, int r, int pos) {
	x = ++tot; lc[x] = lc[y]; rc[x] = rc[y]; siz[x] = siz[y];
	if (l == r) { mx[x] = pre[x] = suf[x] = 0; return; }
	int mid = (l + r) >> 1;
	if (pos <= mid) Change(lc[x], lc[y], l, mid, pos);
	else Change(rc[x], rc[y], mid+1, r, pos);
	Update(x);
}
PII Query(int x, int l, int r, int ll, int rr) {
	if (ll <= l && r <= rr) {
		ans = max(ans, mx[x]);
		return MP(pre[x], suf[x]);
	}
	int mid = (l + r) >> 1;
	PII L(0, 0), R(0, 0);
	if (ll <= mid) L = Query(lc[x], l, mid, ll, rr);
	if (rr > mid) R = Query(rc[x], mid+1, r, ll, rr);
	ans = max(ans, L.second + R.first);
	return MP(L.first + (L.first == siz[lc[x]] ? R.first : 0), R.second + (siz[rc[x]] == R.second ? L.second : 0));
}
void Build(int &x, int l, int r) {
	x = ++tot;
	siz[x] = pre[x] = suf[x] = mx[x] = r - l + 1;
	if (l == r) {
		lc[x] = rc[x] = 0;
	} else {
		int mid = (l + r) >> 1;
		Build(lc[x], l, mid);
		Build(rc[x], mid+1, r);
	}
}
void Prepare() {
	n = getint();
	for (int i = 1; i <= n; ++i) {
		A[i] = getint();
		M[A[i]] = 0;
	}
	for (map<int, int>::iterator it = M.begin(); it != M.end(); ++it) {
		it->second = ++cnt;
		H[cnt] = it->first;
	}
	for (int i = 1; i <= n; ++i) {
		A[i] = M[A[i]];
		ins(A[i], i);
	}
	Build(root[1], 1, n);
	for (int i = 2; i <= cnt; ++i) {
		root[i] = root[i-1];
		for (int j = fst[i-1]; j; j = list[j].next)
			Change(root[i], root[i], 1, n, list[j].data);
	}
}
int x, y, w, l, r, mid;
int main() {
	Prepare();
	for (int Q = getint(), i = 0; i < Q; ++i) {
		x = getint(); y = getint(); w = getint();
		l = 1; r = cnt; 
		while (l < r) {
			mid = (l + r + 1) >> 1;
			ans = 0; Query(root[mid], 1, n, x, y);
			if (ans >= w) l = mid;
			else r = mid - 1;
		}
		printf("%d\n", H[l]);
	}
}